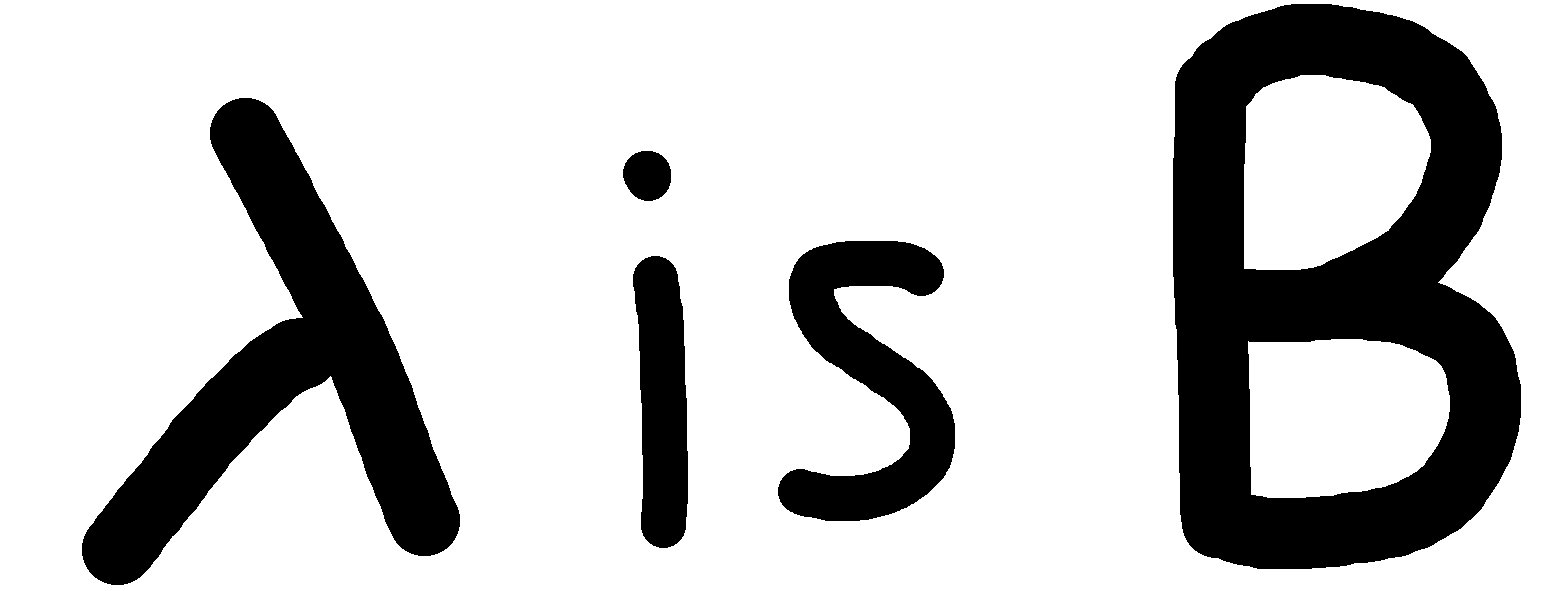Sequences are special functions that map the indices 1 to n to values.
Literals
The empty sequence can be written in B as follows:
B => <>
#{}
B => []
#{}
A sequence containing elements looks like:
B => [42, 1337, 97]
#{[1 -> 42] [2 -> 1337] [3 -> 97]}
In lisb style:
lisb=> (sequence) ;; B: []
#{}
lisb=> (sequence 42 1337 97) ;; B: [42, 1337, 97]
#{[1 -> 42] [2 -> 1337] [3 -> 97]}
Sets of Sequences
Note that the following expressions construct all possible sequences mapping to the values of the set. Thus, there are infinitely many.
lisb=> (seq #{1337 42}) ;; B: seq({1337, 42})
#{#{[1 -> 42] [3 -> 42] [2 -> 42]} #{[1 -> 42] [2 -> 42]} #{[3 -> 1337] [1 -> 42] [2 -> 42]} #{[2 -> 1337] [3 -> 1337] [1 -> 42]} #{[2 -> 42] [3 -> 42] [1 -> 1337]} #{} #{[1 -> 42]} #{[2 -> 1337] [1 -> 42]} #{[2 -> 42] [1 -> 1337]} #{[1 -> 42] [3 -> 42] [2 -> 1337]}}
lisb=> (seq1 #{1337 42}) ;; B: seq1({1337, 42})
#{#{[1 -> 42] [2 -> 42] [3 -> 1337]} #{[1 -> 42] [2 -> 42]} #{[3 -> 42] [2 -> 42] [1 -> 42]} #{[3 -> 42] [2 -> 1337] [1 -> 42]} #{[1 -> 42] [2 -> 1337]} #{[1 -> 1337]} #{[2 -> 1337] [1 -> 42] [3 -> 1337]} #{[3 -> 42] [1 -> 1337] [2 -> 42]} #{[1 -> 42]} #{[2 -> 42] [1 -> 1337]}}
lisb=> (and (subset? :x (seq #{1337 42})) (= (card :x) 5)) ;; B: x<:seq({1337, 42}) & card(x)=5
{:x #{#{[1 -> 42] [3 -> 1337] [2 -> 42]} #{[3 -> 42] [2 -> 42] [1 -> 42]} #{} #{[2 -> 42] [1 -> 42]} #{[1 -> 42]}}}
lisb=> (and (subset? :x (seq1 #{1337 42})) (= (card :x) 5)) ;; B: x<:seq1({1337, 42}) & card(x)=5
{:x #{#{[1 -> 42]} #{[3 -> 1337] [2 -> 42] [1 -> 42]} #{[2 -> 42] [1 -> 42] [3 -> 42]} #{[1 -> 42] [2 -> 42]} #{[1 -> 42] [2 -> 1337]}}}
Injective Sequences
lisb=> (iseq #{1337 42}) ;; B: iseq({1337, 42})
#{#{[2 -> 1337] [1 -> 42]} #{} #{[1 -> 1337]} #{[2 -> 42] [1 -> 1337]} #{[1 -> 42]}}
lisb=> (iseq1 #{1337 42}) ;; B: iseq1({1337, 42})
#{#{[1 -> 42]} #{[1 -> 1337]} #{[2 -> 1337] [1 -> 42]} #{[1 -> 1337] [2 -> 42]}}
Bijective Sequences (Permutations)
lisb=> (perm #{1337 97 42}) ;; B: perm({1337, 97, 42})
#{#{[2 -> 42] [3 -> 1337] [1 -> 97]} #{[1 -> 1337] [2 -> 42] [3 -> 97]} #{[1 -> 42] [2 -> 1337] [3 -> 97]} #{[1 -> 42] [2 -> 97] [3 -> 1337]} #{[3 -> 42] [1 -> 97] [2 -> 1337]} #{[2 -> 97] [1 -> 1337] [3 -> 42]}}
Size of Sequence
lisb=> (size (sequence 1 2 3 4)) ;; B: size([1, 2, 3, 4])
4
Getting Longer
lisb=> (concat (sequence 4 3 2) (sequence 6 7 8)) ;; B: [4, 3, 2]^[6, 7, 8]
#{[5 -> 7] [2 -> 3] [1 -> 4] [4 -> 6] [6 -> 8] [3 -> 2]}
lisb=> (prepend 0 (sequence 6 7 8)) ;; B: 0->[6, 7, 8]
#{[1 -> 0] [4 -> 8] [3 -> 7] [2 -> 6]}
lisb=> (append (sequence 6 7 8) 0) ;; B: [6, 7, 8] <- 0
#{[2 -> 7] [4 -> 0] [3 -> 8] [1 -> 6]}
lisb=> (conc (sequence (sequence 42 1337) (sequence 1 2) (sequence 9 9))) ;; B: conc([[42, 1337], [1, 2], [9, 9]])
#{[5 -> 9] [2 -> 1337] [4 -> 2] [6 -> 9] [1 -> 42] [3 -> 1]}
Reversing a Sequence
lisb=> (reverse (sequence 1 2 3)) ;; B: rev([1, 2, 3])
#{[2 -> 2] [3 -> 1] [1 -> 3]}
Getting Shorter
lisb=> (front (sequence 1 2 3)) ;; B: front([1, 2, 3])
#{[1 -> 1] [2 -> 2]}
lisb=> (drop-last (sequence 1 2 3)) ;; B: front([1, 2, 3])
#{[2 -> 2] [1 -> 1]}
lisb=> (tail (sequence 1 2 3)) ;; B: tail([1, 2, 3])
#{[1 -> 2] [2 -> 3]}
lisb=> (rest (sequence 1 2 3)) ;; B: tail([1, 2, 3])
#{[1 -> 2] [2 -> 3]}
Accessing
lisb=> (first (sequence 1 2 3)) ;; B: first([1, 2, 3])
1
lisb=> (last (sequence 1 2 3)) ;; B: last([1, 2, 3])
3